Au 12e siècle, les savoirs géométriques sont divers entre spéculations et pratiques, sans que les unes s’opposent aux autres. Les sources de ces savoirs sont plurielles entre une continuité apparente du monde latin et une indéniable appropriation des pays d’Islam à partir de la traduction et l’assimilation d’un corpus de textes arabes venant « combler la pénurie des latins ». Ainsi, à l’aube de la naissance de l'université médiévale, la géométrie — un des arts du quadrivium — est profondément transformée tant dans ses contenus que ses méthodes. L’objet de la conférence est de donner à voir cette géométrie à partir d’une sélection de textes qui nous permettra de retracer modestement la lente élaboration de la discipline.

La conférence évoquera les bouleversements de l’enseignement de la géométrie au Japon pendant l’ère Meiji (1868-1912), notamment la question du langage et de la démonstration, et leurs liens avec l'enseignement actuel de la démonstration.

On insiste souvent, à juste titre, sur l’articulation à l’oeuvre chez Descartes entre méthode et pratique de la géométrie, en prenant pour objet d’étude privilégié la Géométrie de 1637. L’objet de cet exposé est d’éprouver cette articulation en considérant d’autres géométries cartésiennes, à savoir la géométrie de la Correspondance et l'édition latine de la Géométrie de 1659-1661 donnée par Schooten. À l’aune de ce corpus, je me propose de traiter quelques-uns des thèmes classiques cartésiens (l’importance du symbolisme, le refus de l’infini) en apportant un léger contrepoint aux thèses de l’historiographie. Je ferai voir en particulier que les pratiques cartésiennes de résolution des problèmes géométriques au moyen de l’analyse algébrique ne se conforment pas toujours à la méthode de 1637 et que celle-ci évolue avec celles-là, après la publication de la Géométrie, quoiqu’en dise son auteur. L’exposé sera l’occasion de présenter des textes mathématiques originaux (des imprimés mais aussi des manuscrits), certains connus et d'autres moins connus, du dix-septième siècle. Je terminerai en essayant de donner quelques pistes d’utilisation de tels textes dans l’enseignement secondaire, mais aussi universitaire, des mathématiques.

Le XIXe siècle est le théâtre à la fois de l'institutionnalisation de l'enseignement secondaire, et de travaux novateurs des géomètres conduisant à repenser la notion de méthode. Cette conférence présente les nouveaux problèmes et les nouvelles méthodes qui apparaissent alors dans les ouvrages d'enseignement secondaire de la géométrie, en tâchant d'analyser les conceptions et les motivations à l’œuvre derrière les choix innovants.

Dans le monde arabo-musulman, la période 1700-1900 se caractérise par la cohabitation d’un système éducatif traditionnel sclérosé et d’une multiplicité de germes de renouveau. Dans le domaine de la géométrie (al-handasa), les plus élémentaires des manuels anciens demeurent à l’étude pendant qu’on rédige de nouveaux ouvrages utiles aux arpenteurs, artilleurs ou cartographes. Un immense mouvement de traduction scientifique voit naître, au Caire, à Tunis, Marrakech, Beyrouth ou Calcutta des versions arabes d’ouvrages géométriques étrangers de niveaux variés. Nous présenterons quelques-uns de ces étonnants manuscrits, dont certains n’ont été découverts que très récemment. Nous insisterons sur les buts qu’ils poursuivaient et les méthodes qu’ils préconisaient, tout en essayant d’évaluer leur usage effectif et leur impact.

• Naṣīr al-dīn al-Ṭūsī (m. 1274), Recension du livre des éléments de géométrie d’Euclide
• Ghiyāth al-dīn al-Kāshī (m. 1429), La Clef du calcul
• Qāḍī Zāda al-Rūmī (m. 1436), Commentaire sur le livre des théorèmes fondamentaux d’al-Samarqandī
• Bahā’ al-dīn al-‘Āmilī (m. 1621), La Quintessence du calcul ‘Abd al-laṭīf al-Dimashqī, Le fruit sélectionné dans la science du mesurage, 1720
• Muḥammad al-Aqkirmānī, Épître sur la connaissance des distances, 1755
• ‘Uthmān Efendi, Le cadeau du converti pour ranimer la flamme éteinte, 1779
• Sulaymān al-Ḥarā’irī, Résultats rationnels en géométrie pratique, v. 1840
• traduction arabe des Éléments de géométrie de Legendre
• traduction arabe du Traité analytique des sections coniques du marquis de L’Hôpital
• traduction arabe du Traité élémentaire de trigonométrie rectiligne et sphérique, et d’application de l’algèbre à la géométrie de Lacroix
• traduction arabe du Toisé théorique et pratique ou Art de mesurer de G.F. Olivier
• traduction arabe de l’Abrégé de géométrie pratique appliquée au dessin linéaire, au toisé et au levé des plans des Frères des écoles chrétiennes
• traduction arabe du Cours de géométrie élémentaire [...] suivi de notions sur le levé des plans et l’arpentage d’Adrien Guilmin

Dans sa volonté de corriger ce qu’il pensait être des insuffisances des Éléments d’Euclide, Girolamo Saccheri a publié en 1733 l’ouvrage intitulé Euclides ab omni nævo vindicatus... divisé en deux livres. Dans le premier, il cherche à démontrer, après plusieurs tentatives de savants depuis l’Antiquité, le cinquième postulat, souvent appelé postulat des parallèles, et dans le second, à établir une définition, satisfaisante selon lui, de l’égalité des rapports ou proportion. Cet exposé ne s’attachera qu’à une présentation du premier livre dans la perspective d’une traduction de l’ouvrage du latin en français. Ïl montrera que, dans sa quête d’une contradiction dans le cas d’un refus du inquième postulat, Saccheri a établi, avec une rigueur logique (presque) parfaite, trente-neuf propositions qui, environ un siècle plus tard, feront partie du corpus de la géométrie hyperbolique inventée et publiée en tant que théorie nouvelle par Lobatchevski puis Bolyaï.

L’enseignement de la géométrie a connu de nombreux soubresauts au cours du XXe siècle, en France et ailleurs, posant des questions récurrentes : quelle géométrie ? Comment l’enseigner ? Géométrie pour tous (et toutes) ? Un aperçu historique à travers les programmes, des manuels, les échanges relatés par exemple dans la revue L’enseignement mathématique, permettra d’aborder ces questions, qui sont toujours d’actualité.

• Manuels de géométrie de l’enseignement secondaire « long », de l’enseignement technique, du primaire supérieur,
• les différents programmes de mathématiques du XXe siècle,
• des extraits significatifs de la revue de l’APMEP et de la revue L’enseignement mathématique, …

L’exposé porte sur de « grands » textes sur l’aire du disque, dont la connaissance fait partie de la culture générale d’un enseignant/formateur en mathématiques. Il prendra la forme d’une lecture commentée de textes bien connus des historiens des mathématiques mais qui demeurent difficiles d’accès au débutant. Les textes sont a priori trop difficiles pour un usage direct en classe. On pourra, dans un dernier temps, s’interroger sur leur adaptation à l’enseignement ou à la formation.

• Archimède La mesure du cercle.
• Leibniz : la méthode des métamorphoses dans Histoire et origine du calcul différentiel.
• Arnaud Nouveaux éléments de géométrie (théorème 5, p.310-311 de l’édition de 1667, disponible sur Gallica).

Chacun sait que les Éléments d’Euclide ont été rédigés par un énigmatique savant du Museion d’Alexandrie, sorte de Bourbaki du IIIe siècle avant notre ère. Commentés, augmentés, critiqués, ils sont pourtant restés pendant 2000 ans la base même de l’enseignement des mathématiques, alors que celles-ci s’enrichissaient constamment de nouvelles disciplines. Pourtant bien informés des développements de celles-ci, d’innombrables savants sont restés fascinés par les Eléments au point de les traduire dans diverses langues. Bien entendu, il y avait souvent, derrière ce projet, des visées politiques ou religieuses. Ainsi, des missionnaires jésuites bien formés en science furent envoyés en Chine pour y réorganiser l’astronomie de l’Empereur, c’est pourquoi il existe une version chinoise des Eléments. Une tentative comparable eut lieu en Inde, à l’occasion de l’aide scientifique demandée aux puissances coloniales par le rāja Jai Singh II (1688-1743) de Jaipur. Il faut dire qu’avant de recourir à celles-ci, Jai Singh s’était déjà bien informé sur les mathématiques et l’astronomie ‘classiques’, faisant traduire du persan en sanskrit l’Almageste et les Eléments. Nous illustrerons notre propos par quelques extraits comparés de différentes versions.

• Eléments d’Euclide, versions diverses (grecque, latines,...), en particulier :
• Taḥrīr kitāb uṣūl al-handasa de Naṣīr ad-Dīn aṭ-Ṭūsī, ‘traduction’ en arabe/persan des Eléments Rekhāgaṇita de Jagannātha Saṃrāṭ, traduction en sanskrit des Eléments

À l’école, au collège, comment doit-on parler de la droite, du segment, du point, du carré pour être « en accord avec les mathématiques » ? Une telle phrase (posée parfois par les enseignants aux formateurs) accorde une existence objective à ces objets, à tout le moins dans une théorie mathématique, dans ce que nous reconnaissons comme une pensée relevant d’une forme de réalisme. L'opposition entre des réalismes de type aristotélicien et platonicien est souvent considérée comme non discriminante des pratiques des chercheurs en mathématiques. Qu’en est-il pour l’exploration de questions d’enseignement et d’apprentissage ? Notre exposé développe les prémisses d’une analyse épistémologique des conceptions de la géométrie, orientée vers l'éclairage de faits didactiques. Nous mettrons en particulier en défaut l’idée que la géométrie prescrite par les nouveaux programmes du cycle 3 puisse convoquer une conception des objets géométriques vus comme objets objectifs, indépendants de l’activité humaine, qu’il suffit de "dire bien" pour enseigner efficacement. Nous interrogerons alors les niveaux de conceptualisation possibles de ces objets à l’école en lien avec les pratiques géométriques qui les vont vivre.

• Les sulbasutras de Baudhayana, Apastamba, Katyayana et Manava, texte, traduction anglaise et commentaires de S. N. Sen et A. K. Bag, Indian National Science Academy, New-Dehli, 1983.
• Euclide, Les Éléments, vol. 1 à 4, notes et commentaires par Bernard Vitrac, Paris, 1994.
• Claude Ptolémée, Composition mathématique, traduction Halma, notes de Delambres Paris, 1813 et édition complète de Heiberg, 1898.
• Felix Klein, Vergleichende Betrachtungen über neuere geometrische Forschungen, dit programme d’Erlangen, Erlangen, Verlag von Andreas Deichert, 1872.
• David Hilbert, Grundlagen der Geometrie, Leipzig, 1903.
• Henri Poincaré, La Science et l’Hypothèse, Paris, 1902.

Les structures cristallines sont des arrangements spatiaux ayant une forme tridimensionnelle. La classification de leurs propriétés mathématiques et géométriques a été systématiquement développée au cours des deux premières décennies du XIXe siècle ; cette classification a été le point de départ d'une longue tradition d'analyse structurelle en cristallographie, lorsque de nouvelles institutions, techniques et pratiques ont été développées (par, par exemple, René Just Haüy ou Christian Samuel Weiss). En examinant le travail de Friedrich Fröbel, qui a aussi travaillé avec Weiss, j'ai l'intention de montrer historiquement le transfert de connaissances de la cristallographie aux activités de jardin d'enfants, activités qui sont développées par Fröbel, en montrant que la plupart, sinon la totalité, de ces activités étaient de nature mathématique et influencées par la cristallographie. En me concentrant sur une activité spécifique de Fröbel, le pliage du papier, je montrerais dans la deuxième partie de mon exposé comment cette activité a été pensée par Fröbel comme un moyen de transmettre des concepts mathématiques aux enfants. Fröbel considérait le pliage du papier comme un moyen d'enseigner aux enfants des concepts abstraits tels que le nombre, la fraction et la similarité des formes, sans les introduire explicitement comme des concepts mathématiques.

• Haüy RJ (1784) Essai d’une théorie sur la structure des crystaux. Gogué & Neé de la Rochelle : Paris.
• Haüy RJ (1801) Traité de minéralogie, premier tome, Louis : Paris.
• Fröbel F (1874 [1850]) « Anleitung zum Papierfalten », dans : Fröbel F, Gesammelte pädagogische Schriften, p. 371–388, Enslin : Berlin. (une traduction en anglais sera fournie)

Notre expérimentation (renouvelée maintenant) a débouché sur l’écriture d’un chapitre du livre Passerelles : enseigner les mathématiques par leur histoire au cycle 3, Arpeme. Cette expérimentation s’est déroulée en CM2 et en 6ème. Les élèves ont étudié le problème de la duplication du carré à travers un extrait du Ménon de Platon. L’objectif est double : faire travailler les élèves sur ce problème de duplication mais également sur la compréhension de texte. Nous avons choisi de travailler sur l’extrait, sans l’alléger ni le modifier, bien qu’il soit d’un abord difficile. Pour le travailler, nous sommes allés chercher renfort du côté de la didactique du français, plus spécifiquement des écrits de Cèbe & Goigoux sur la compréhension de texte ; ils nous ont été utiles pour découper nos séances, le texte et partant ses problèmes mathématiques afin de les rendre accessibles aux élèves. Nous souhaitons en rendre compte dans notre exposé. Les usages de ce texte en cours de Mathématiques ne sont pas rares, mais ils bifurquent souvent vers un travail numérique d’approximation de la longueur de la diagonale du carré, alors que nous avons choisi de travailler, à l’image de Socrate, sur la figure, les grandeurs, souvent par découpage et recollement. Les élèves ne rencontrent pas pour la première fois la plupart des notions mathématiques du texte, ils se retrouvent en position d’expert pour lever les ambiguïtés du vocabulaire géométrique et justifier et confirmer mathématiquement des affirmations de Socrates ainsi que sa solution au problème. La traduction en langage géométrique moderne des instructions de Socrate tient une grande place dans notre travail. L’atelier est plus particulièrement conçu pour les enseignants du premier degré.

• Extrait de l’ouvrage Ménon de Platon. Dialogue entre Ménon, Socrate et un esclave de Ménon autour du problème du doublement de l’aire du carré.

Une visite guidée de l’exposition Maths & Puzzles (panneaux à réserver auprès de la Régionale APMEP Poitou Charentes) pour voir que la géométrie, au travers de l’histoire, a permis de mettre au point formules et algorithmes, de résoudre des problèmes du second et du troisième degré, de mettre au défi la logique et le raisonnement des hommes. Nous en verrons des exemples divers, en arithmétique, en algèbre et en géométrie. Cette géométrie peut être matérialisée sous forme de puzzles à manipuler ou à réaliser. La déambulation s’appuiera sur les textes évoqués sur les panneaux de l’exposition.

• L’introduction arithmétique de Nicomaque de Gérase,
• l’Abrégé du calcul d’Al Khwarizmi,
• l’Algèbre de Bombelli,
• Sur ce qui est indispensable aux artisans dans les constructions géométriques d’Abul Wafa,
• Diversions et digressions de Lewis Caroll,
• The Canterbury tales de Dudeney.

En 1890, Gaston Albert Gohierre de Longchamps, professeur au Lycée Charlemagne, écrit un Essai sur la géométrie de la règle et de l’équerre, qu’il considère comme un chapitre d’un Traité de Géométrie pratique. Mais il s’agit d’un manuel s’adressant à ses collègues professeurs et à leurs élèves, qui « y trouveront la matière de nombreux exercices intéressants ». Gohierre de Longchamps explique le choix de la règle et de l’équerre et il montre que l’intérêt pédagogique réside, pour un exercice donné, dans la diversité des solutions possibles et dans la richesse des discussions que ces solutions soulèvent. Il présente des solutions déjà connues et d’autres de son propre cru. Toute la seconde partie de l’ouvrage est consacrée « aux problèmes d’arpentage » et nous proposons d’examiner, parmi ceux-ci, des problèmes de figures inaccessibles, c’est-à-dire dont des éléments nécessaires à la solution ne figurent pas sur la feuille de papier. L’atelier demande des notions rudimentaires de géométrie, telles que les cas d’égalité des triangles.

• Gaston Albert Gohierre De Longchamps, Essai sur la géométrie de la règle et de l'équerre, Paris, Delagrave, 1890.

La duplication du cube se ramenant à l’insertion de deux lignes moyennes proportionnelles entre une ligne et la ligne de longueur double, la difficulté, ou plutôt l’obstacle, réside dans la construction exacte des lignes et non dans les justifications du fait que, sur une figure supposée construite, les lignes montrées sont bien les lignes cherchées. Au premier livre de son De Arte Magna libri quatuor (Paris, 1577), Guillaume Gosselin adjoint à son travail soigné d’algébrisation des règles de fausses positions un chapitre inattendu consacré à une extension de la règle de fausse position double au champ géométrique – envisageable dans la mesure où les sommes, les différences, et les proportionnalités de lignes sont constructibles – pour la résolution, précisément, de la duplication du cube. Michael Stifel s’est également penché, avant Gosselin, sur le problème de la duplication du cube, au deuxième livre de son Arithmetica Integra (Nuremberg, 1544), intitulé « Sur les nombres irrationnels », dans lequel il procède à une lecture arithmétique du dixième livre des Éléments d’Euclide, donnant à voir les nombres irrationnels en les « contractant » sur des figures géométriques.
Ce sont donc des outils mathématiques élémentaires, mais riches des contraintes accompagnant leur utilisation, qui sont mobilisés pour la résolution de ce « problème impossible de l’Antiquité » qui continuera de retenir l’attention jusqu’à ce que Pierre-Laurent Wantzel démontre en 1837 que la racine cubique de 2 n’est pas constructible à la règle et au compas.

• Guillaume Gosselin, De Arte Magna libri quatuor, Paris, 1577
• Guillaume Gosselin, L’Arithmetique de Nicolas Tartaglia, Paris, 1578
• Michael Stifel, Arithmetica Integra, Nuremberg, 1544

La fin du XIXe siècle est une période où l’on redécouvre certains écrits théoriques de l’histoire de la perspective, comme le De prospectiva pingendi de Piero della Francesca. La première édition imprimée de son traité manuscrit, accompagnée d’une traduction allemande, paraît à Strasbourg en 1899. Parmi les commentateurs, historiens d'art se disant démunis ou historiens des sciences pratiquant une certaine “philosophie spontanée des savants”, passablement rétrospective, s’élève une voix singulière : celle d’Eugène Rouché, qui, comme Michel Chasles, a lu attentivement la littérature perspective. Relisons-le : il nous livres des clefs précieuses, qui le conduisent pourtant à certaines conclusions contestables. La chose est intéressante, car récurrente dans une histoire du regard et de l’aspect souvent déviée par des points aveugles – y aurait-il des trous noirs en épistémologie ? –, et peu capable de regards obliques et croisés.

• Eugène Rouché, « Les Origines du trait de perspective », 1891.
• Ouvrage(s) de Michel Chasles, traités de Piero della Francesca, Jean Pélerin le Viator, Albrecht Dürer, Sebastiano Serlio, Samuel Marolois.

L'exposé se proposera de présenter les points essentiels des programmes de 1970 afin d'en analyser les motivations et les dérives. Il s'attachera ensuite à décrire les retours en arrière liés à la « contre-réforme » et à chercher les influences que ces programmes peuvent avoir gardées sur la situation actuelle.

• Instructions et manuels.

Les Neuf chapitres, le classique mathématique de la Chine ancienne présenté et traduit par Karine Chemla et Guo Shuchun, permettent de se faire une idée assez précise des préoccupations mathématiques des hommes d’ un endroit donné et à un moment donné, l’un et l’autre fort éloignés de nous. En classe de Troisième, dans le cadre d’un EPI intitulé « Fabriquons un puzzle 3D », la présentation en particulier du chapitre 5 de cet ouvrage donne à voir (contrairement à l’ouvrage original qui ne comporte pas de figures) des figures familières aux élèves : cubes, pavés, pyramides, prismes …. On peut aussi y voir des figures plus complexes que celles abordées habituellement dans les manuels scolaires : des exemples de décompositions en perspectives de ces différents solides. La proposition faite alors aux élèves est la suivante : parmi les solides qui vous sont familiers, choisissez-en un et imaginez-vous aussi pour ce solide une décomposition, puis procédez à la fabrication du puzzle correspondant. Le cœur de l’exposé sera un compte-rendu de la façon dont s’est déroulé cet EPI en insistant en particulier sur l’usage de Sketchup (en co-intervention avec le professeur de technologie) comme outil d’exploration et de conception du puzzle ainsi qu’en présentant les difficultés rencontrées, mais aussi les perles produites par certains groupes.

• Les Neuf chapitres, le classique mathématique de la Chine ancienne, présenté et traduit par Karine Chemla et Guo Shuchun, chapitre 5.

Euclide et Liu Hui ont préparé le terrain. Deux voies historiques pour parler du volume de la pyramide. Nous allons explorer les travaux de ces maîtres, puis innover. Peut-on les réunir, fusionner leurs chemins, en trouver un prolongement ? Et permettre aux élèves de tous âges de manipuler des objets, pour se montrer un théorème avec les mains et les yeux. Tel est le jeu, et l'enjeu. Des mathématiques à voir et à toucher.

• Euclide, livres XI et XII, propositions 11.28 et 12.3 12.4
• Liu Hui, Les Neuf chapitres (discuter les travaux, sa théorie des volumes avec le yangma et le bienao)

L’exposé s’appuie sur une recherche ayant pour finalité de retrouver les connaissances et les gestes professionnels des artisans de l’Antiquité qui ont réalisé les décors géométriques encore visibles aujourd’hui (mosaïque, peinture, stuc), sujet sur lequel il n’existe aucun document écrit ou graphique contemporain. Il s’agit, à partir de l’analyse des seuls documents disponibles (photos, relevés), de tenter de restituer les modèles ayant servi à mettre en place ces décors. Cette recherche débouche sur la proposition d’un modèle vraisemblable – et contrôlable −, d’en proposer un (des) algorithme(s) de construction et, au-delà, une procédure de mise en place in situ à l’aide des instruments de l’époque : cordeau, règle non graduée, équerre. Le principe et les conditions de la démarche, ainsi que les résultats obtenus, seront illustrés par des exemples.
On conclura en suggérant qu’une démarche analogue peut être entreprise dans les classes – et en formation d’enseignants − dans le but de mettre en œuvre et d’articuler les différents paradigmes géométriques de l’enseignement obligatoire.

• Barbet, A. & Parzysz, B. (2015) Peintures d’Hadrumetum. Néréides sur monstres marins : essai de restitution. Revue Tunisienne d’Archéologie n° 2, pp. 75-93.
• Blanc, N. & Parzysz, B (2013). A puzzling set of stucco coffers from Portici. Archaeology and mathematics working together. Nexus Network Journal vol. 15/2. Ed. Birkhaüser (Basel), pp. 209-225.
• Eristov, H. & Parzysz, B. (2018) Une intrigante lame d’ivoire pompéienne. Rivista di Studi Pompeiani XXIX. L’Erma di Bretschneider, Roma, pp. 21-29.
• Malek, A.-A., Parzysz, B. (2016) Les mosaïques « kaléidoscopiques » de Numidie. Bulletin de l’APMEP 521, 554-561.
• Parzysz, B. (2009) Key digrams to design and construct Roman geometric mosaics? Nexus Network Journal 11/2, pp. 273-288. Ed. Birkhaüser, Basel.
• Parzysz, B. (2012) Une grande famille de décors géométriques. Proceedings of the 11th International colloquium on ancient mosaics (M. Šahin, ed.). Ed. Zerobooks (Istanbul), pp. 735-748.
• Parzysz, B. (2014) Une composition géométrique étonnante : la mosaïque de Lod (Israël). Bulletin de l’APMEP 509, pp. 295-308.
• Parzysz, B. (2017) La géométrie des mosaïques de Neptune et de Méduse : thèmes, variations, adaptations. Le quartier antique du Palatium et ses domus. Archéologie au collège Lumière à Besançon (Doubs) (C. Munier, dir.). Presses Universitaires de Franche-Comté, Besançon, 289-297.
• Vitruve, De l’architecture. Livre 7. I. De la rudération. Trad. Ch.-L. Maufras, tome second, 119-123. Ed. Pancoucke, Paris 1847

Jules Houël (1823-1886) étudie à l’École normale en 1843-1846 puis enseigne – notamment la géométrie élémentaire – en lycée, quelques années. Cette expérience le conduit à réfléchir à la fois sur les fondements de la géométrie (élémentaire) et sur les traités de géométrie existant. Il publie le fruit de ses réflexions dans un article en 1863 paru aux Archiv der mathematik und Physik sous le titre « Essai d'une exposition rationnelle des principes fondamentaux de la Géométrie », puis en 1867 dans son mémoire Essai critique sur les principes fondamentaux de la géométrie élémentaire ou commentaire sur les XXXII premières propositions des Eléments d'Euclide publié chez Gauthier-Villars. Nous verrons que Houël prône un enseignement de la géométrie basé sur une approche expérimentale et une version revisitée des Éléments d’Euclide et qu’il propose d’enseigner le reste des mathématiques du secondaire à partir de la géométrie.

• Euclide, Éléments, t.I, Paris, CNRS Éditions (G.-J. Kayas), 1979.
• Houël, Jules, « Essai d'une exposition rationnelle des principes fondamentaux de la Géométrie », Archiv der Mathematik und Physik, t.XI, Greifswald, 1863, pp.171-221.
• Houël, Jules, Essai critique sur les principes fondamentaux de la géométrie élémentaire ou commentaire sur les XXXII premières propositions des Eléments d'Euclide, Paris, Gauthier-Villars, 1867.
• Legendre, Adrien-Marie, Éléments de géométrie, Paris, Firmin Didot, 1794.
• Rouché, Eugène, Comberousse (De), Charles, Traité de géométrie élémentaire, Paris, Gauthier-Villars, 1866.

La géométrographie ou art des constructions géométriques (Lemoine, 1902) est une proposition de mesure de complexité des constructions à la règle et au compas (et équerre). GéoTortue (Tummarello, 2008) est un logiciel inspiré de LOGO qui permet d’écrire des programmes simples pour dessiner des figures géométriques à l'aide d'une tortue se déplaçant sur l'écran. Nous nous intéressons ici aux instructions élémentaires papier-crayon versus écran-tortue pour dégager les différents points de vue géométriques apportés par ces deux approches et la richesse de leur complémentarité, en particulier pour la construction du cercle et la définition des angles. Installation de GéoTortue à prévoir.

• Lemoine E. (1888) De la mesure de la simplicité dans les sciences mathématiques, Actes du congrès d’Oran de l'AFAS de 1888, vol 2, 75-95
• Lemoine E. (1902) Géométrographie, ou art des constructions géométriques, Paris : C. Naud
• Papert S. (1980) Mindstorm : Children, computers and powerful ideas. New York :basic Books. Traduit en 1981 par Vassello-Vilaneau sous le titre Le jaillissement de l’esprit : ordinateur et apprentissage ? Paris : Flammarion

Au XVIe siècle fleurissent en France un grand nombre de livres de géométrie pratique. Au bâton de Gerbert plus ancien, viennent s'ajouter carré géométrique, équerre articulée, arbalestrille et bien d'autres (croix du bûcheron,…). À travers les textes de Gerbert d'Aurillac et d'Oronce Fine nous nous pencherons sur la conception et l'utilisation de ces instruments. Leur extrême simplicité les rend faciles et peu onéreux à construire et leur prise en main par les élèves donne tout son sens à la géométrie. L'atelier réunira un temps d'étude de texte, un temps d'expérimentation avec ces instruments et un temps d'échange sur leur apport à la classe.

• Gerbert d'Aurillac : Traité de géométrie
• Oronce Fine : Composition et usage du carré géométrique

Nous introduisons les problématiques liées au parallélisme, et montrons comment la géométrie hyperbolique est apparue dans l'histoire. Nous nous focalisons notamment sur les modèles euclidiens de cette géométrie, introduits par Beltrami dans ses travaux, et repris par Klein et Poincaré. En particulier, nous montrons comment il est possible de présenter le disque de Poincaré à des lycéens à l’aide de notions de géométrie élémentaire, et comment il est possible d’utiliser le logiciel geogebra afin de leur faire effectuer des constructions dans ce modèle.

• E. Beltrami, Essai d'interprétation de la géométrie non euclidienne, Annales Scientifiques de l'Ecole Normale Supérieure vol. 6, 1869, p. 251-288.
• L. Boi, L. Giacardi, R. Tazzioli, La découverte de la géométrie non euclidienne sur la pseudosphère. Les lettres d'Eugenio Beltrami à Jules Hoüel (1868-1881), Paris, Blanchard, 1998.
• B. Allart, R. Bkouche, Cours de géométrie à l’usage des (futurs) enseignants, à paraître fin 2017, ellipses.

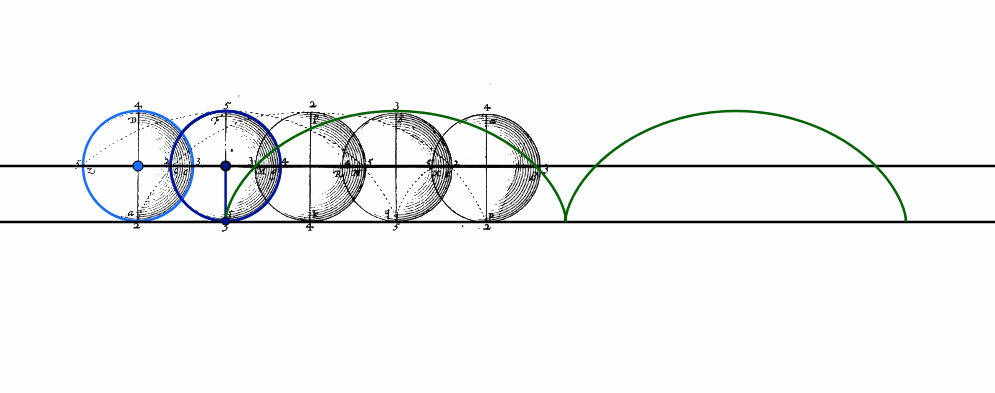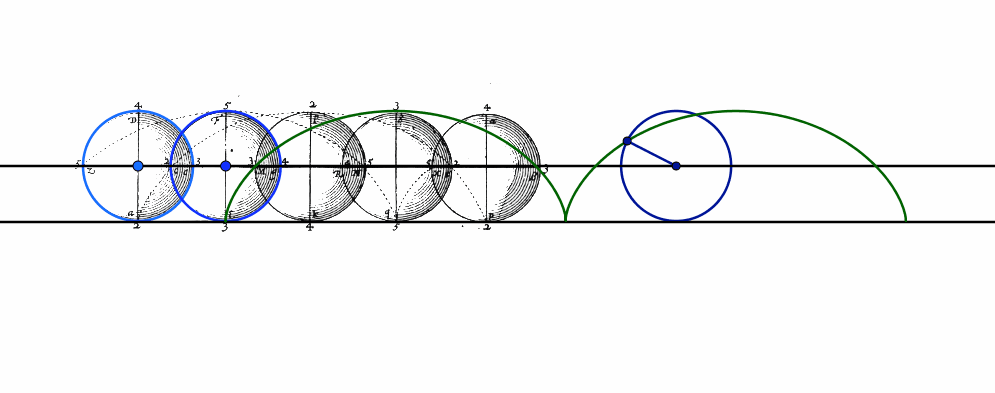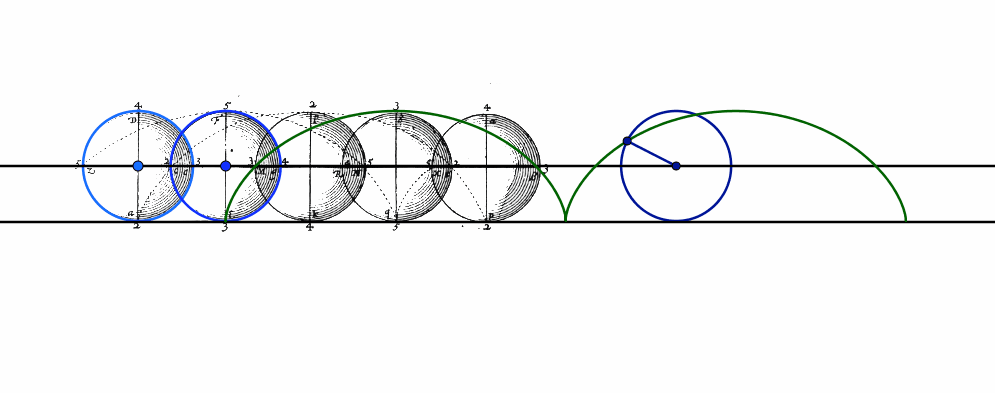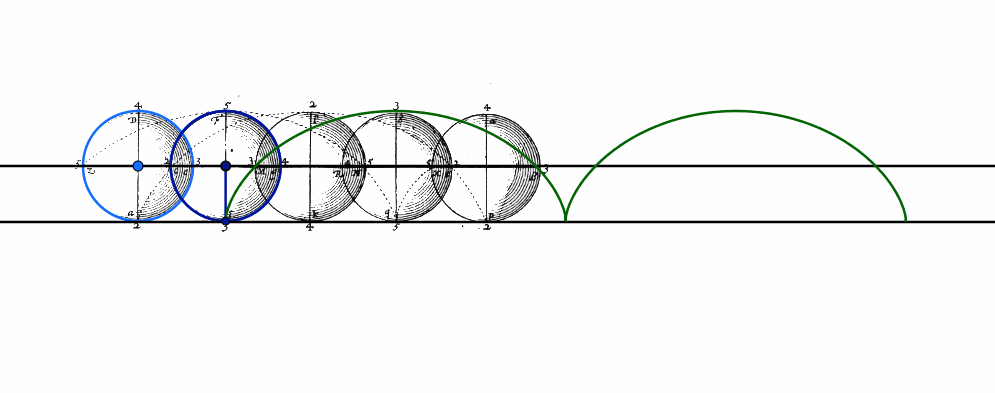
En général, les courbes apparaissent dans l’enseignement comme graphes de fonctions, ce qui constitue un renversement de l’ordre historique. En effet, l’histoire des mathématiques montre que les courbes ont d’abord un intérêt en elles-mêmes, qu’une description géométrique ou une conception cinématique permet de les étudier. Nous le verrons depuis l’Antiquité jusqu’aux inventeurs du calcul infinitésimal Newton et Leibniz, lequel a introduit le terme de fonction, en passant par Descartes, qui définit les courbes géométriques comme celles qui sont décrites par des mouvements bien réglés les uns aux autres. Nous lirons des textes anciens où les courbes sont introduites comme solutions de problèmes géométriques, optiques ou physiques, où elles sont décrites par des mouvements ou des instruments de tracés, de sorte à concevoir un enseignement des courbes lié à des usages et à des instruments et ouvert aux autres disciplines.

• Pappus, La collection mathématique (éd. 1982).
• René, Descartes, La Géométrie et L’optique (1637).
• Frans van Schooten, Organica conicarum sectionum in Plano descriptione Tractatus (1646).
• Gilles Personne de Roberval, Observations sur la composition des mouvements et sur le moyen de trouver des tangentes aux lignes courbes (éd. 1693).
• Christian Huygens, Horologium oscillatorium (1673).
• Erhenfried von Tschirnhaus, Medicina mentis sive artis inveniendi praecepta generali (1687)
• Gottfried Leibniz, La naissance du calcul infinitésimal (éd. 1989).
• Isaac Newton, Organic description of curves (éd. 1860).

L’algorithmique et de la programmation sont aujourd’hui de plus en plus valorisés dans Les programmes de collège et lycée. Quelles sont les conséquences possibles de cette évolution pour l'enseignement de la géométrie ? Dans cet atelier nous aborderons cette question à partir d'un matériel historique ancien et médiéval. Ainsi les mathématiques Chinoises, qui donnent une place centrale à la notion de procédure, indiquent elles un usage de raisonnements géométriques pour justifier ou généraliser des procédures de calcul. Dans l’antiquité gréco-romaine, les textes métrologiques anciens comme ceux de Héron d'Alexandrie sont riches en procédures explicites de calcul, qui sont introduites ou justifiées en se fondant sur la tradition de méthodes géométriques "pures", dans le genre des travaux d'Euclide ou d’Archimède. Ces textes déductifs ont été mis en jeu dès l'antiquité et pendant le Moyen-âge, pour justifier des algorithmes de calcul ou pour permettre de les inventer. Étudier ces textes permet donc de réfléchir à la place que tiennent ou pourraient tenir les raisonnements géométriques, dans l’invention et la justification d’algorithmes. L’atelier demande quelques notions de géométrie élémentaire (cas d’égalité de triangles)

• Extraits des Éléments de géométrie d’Alexis Clairaut, des Métriques de Héron d’Alexandrie, du traité d’algèbre d’al-Khwarizmi et du commentaire de Lui Hui sur les Neuf Chapitres

À la lecture de quelques textes de mathématiques appliquées, il s’agira d’analyser et de mettre en œuvre les méthodes proposées pour calculer des aires simples (polygones irréguliers…). Il sera donc demandé aux participants de vérifier l’exactitude de ces méthodes et de les utiliser sur des exemples simples !

• extrait de la Siensa de Destrar, Boysset(1405)
• extrait de la Géométrie pratique ou l’art de mesurer, Clermont (1693)
• Article « Arpentage » du Dictionnaire des Maths appliquées, Sonnet (1868)
• extrait de l’Arithmétique, arpentage universel… , Jean Abraham (1624)

Les cas d’égalité des triangles sont revenus, après une longue absence, dans les programmes de collège en 2015 ; l’étude de certains textes historiques permet de dégager l’importance de ces cas d’égalité dans les démonstrations de résultats fondamentaux de géométrie élémentaire, ainsi que pour la résolution de problèmes de géométrie. La lecture des Éléments d’Euclide et la façon dont des auteurs de différentes époques se les sont appropriés, les ont modifiés ou critiqués, nous donnent des pistes pour travailler la géométrie en classe avec une progression cohérente, en redonnant toute sa place à la démonstration. En effet, celle-ci devient plus abordable avec l’outil des cas d’égalité, qu’il s’agisse de recherches sur des problèmes ou de résultats à institutionnaliser. L’atelier est prévu pour des enseignant-e-s plutôt débutant-e-s en histoire des mathématiques

• Euclide Les Éléments
• Clairaut, Éléments de géométrie,
• Adrien-Marie Legendre, Éléments de géométrie
• Lacroix, Élémens de géométrie à l’usage de l’École Centrale des Quatre-Nations
• Henri Bos, Géométrie élémentaire

Dans un premier temps, nous illustrerons au travers de deux exemples comment la perspective a permis de porter un regard neuf sur certains chapitres de la géométrie grecque. Nous parlerons de la construction d’un discours unique pour des figures traitées séparément dans les traités grecs et de la mise en avant des propriétés d’incidence. Nous ferons référence à des traités de Girard Desargues et de Brook Taylor. Dans un second temps, les participants seront mis en activité. Nous proposerons, dans le contexte de la perspective, une séquence d’enseignement qui a été utilisée dans nos classes pour l’étude de la géométrie d’incidence figurant au programme des élèves de 16 ans.

• Girard Desargues, Brouillon project d’une atteinte aux evenemens des rencontres du Cone avec un Plan, Paris, 1639.
• Brook Taylor, New Principles of Linear Perspective: or the Art of Designing on a Plane the Representations of all sorts of Objects, in a more General and Simple Method than has been done before, London, 1719.

En 1816, le géomètre de première classe Philogone Barbotin réalise, sous la supervision de l’ingénieur-vérificateur M. Robin, le cadastre de la commune d’Annappes, située à proximité de Lille. Nous chercherons comment s’articulent la construction du cadastre et les savoirs mathématiques de l’époque. Nous manipulerons à la fois des documents locaux (atlas, tableau indicatif, matrices) et des ressources généralistes comme les manuels d’arpentage, les règlements ou les instruments géométriques. Délimitation, canevas trigonométrique et levé de parcelles utilisent des mathématiques élémentaires des cycles 3 et 4. Cette étude de cas donne ainsi une méthode et différents outils pour permettre à chacun de s’approprier les documents cadastraux locaux et les intégrer dans son propre enseignement. Cet atelier s’adresse volontairement à la fois aux enseignants du premier degré et à ceux du second degré. Il demande une salle suffisamment vaste pour réaliser des manipulations variées.

• Documents du cadastre : Atlas, extraits de tableaux indicatifs et de matrices cadastrales.
• Manuels d’arpentage et de levé des plans du XIXe siècle
• Règlements et sources d’archives sur l’organisation du cadastre et la biographie des géomètres
• Instruments (équerre d’arpenteur, chaîne d’arpentage…)

Si la géométrie des arpenteurs du Nil remonte à 3000 ans avant notre ère, si la géométrie euclidienne date du IIIe siècle av. J.-C., si la géométrie analytique est l’œuvre de Descartes en 1637, si la géométrie projective est fondée deux ans plus tard par Desargues et si la géométrie algébrique dérivant traditionnellement des deux dernières prend son essor au XIXe siècle, la géométrie tropicale est à peine âgée d’un demi-siècle. Les courbes tropicales sont des réseaux de segments et de demi-droites comparables aux cytosquelettes des amibes. Elle peut ainsi être considérée comme « une limite possible » de la géométrie classique obtenue en « dégénérant » les objets usuels. La géométrie tropicale a sa propre algèbre, lui permettant de revisiter la géométrie algébrique selon un modèle plus simple. Une belle réussite est le fameux théorème de Bézout sur le nombre de points d’intersection de deux courbes algébriques. Enfin, grâce à la procédure du patchwork, une courbe tropicale peut ressembler à s’y méprendre à une courbe algébrique et cette ressemblance pourrait dans un futur proche avoir raison du 16eme problème de Hilbert !
Le théorème de Bézout (1764). L’atelier est conçu pour les enseignants du second degré. Il demande des connaissances basiques en géométrie analytique (équation de droites, de coniques), en géométrie projective (point à l’infini), en géométrie algébrique, en théorie des graphes, en théorie des corps. Il demande de connaitre aussi la fonction log, la notion de max et de savoir dessiner des fonctions affines par intervalles.

• Le 16e problème de Hilbert (1900).
• Amibes et géométrie tropicale de Mickaël Nicotera (2007).
• Géométries énumératives complexe, réelle et tropicale d’Erwan Brugallé (2007).
• Introduction à la géométrie tropicale de Ilia Itenberg (2008).
• Un peu de géométrie tropicale d’Erwan Brugallé (2009).

Construire un rectangle ou un carré d’aire égale à celle d’une ou plusieurs figures données est un champ de problèmes qui a traversé toutes les civilisations. On y retrouve des problèmes ou théorèmes célèbres comme la quadrature du cercle ou le théorème de « Pythagore », et des méthodes aussi différentes que la construction à la règle et au compas (ou avec une corde) ou le découpage. Ce champ de problèmes permet de comprendre comment les hommes ont pu trouver diverses formules exactes ou approchées pour calculer l’aire de figures simples, comment avec plusieurs carrés égaux ils ont réalisé un seul carré de même aire, comment ils ont trouvé le théorème de « Pythagore ».La plupart des problèmes que nous étudierons permettent de montrer comment une partie de la géométrie et du calcul, des cycles 3 et 4, peut se construire autour de ces problèmes de construction et d’aire. Dans les utilisations, l’atelier est conçu plus spécialement pour des enseignants des cycles 3 et 4. Même si la façon dont sont écrits ces textes anciens peut surprendre, les contenus mathématiques restant élémentaires, leur lecture peut amener à une réflexion pédagogique sur la mise en forme du discours mathématique.

• Baudhayana, Sulbasutras, extraits
• Liu Hui, Les Neuf chapitres, extraits du chapitre 1 « Champs rectangulaires »
• Euclide, Éléments, extraits des livres I et II
• Abul Wafa, Constructions géométriques nécessaires à l’artisan, extraits du chapitre 11
• Dürer, Géométrie, extraits du livre II

Selon Hérodote, l’origine de la géométrie peut être trouvée en Égypte, lors des mesures des terrains après la crue annuelle du Nil. Nous ne devons pas pour autant oublier les réserves de céréales conduisant à des calculs scrupuleux des volumes de greniers, en particulier ceux à base circulaire. Deux documents mathématiques qui nous sont parvenus en sont le témoignage, le Papyrus Rhind et un Fragment d’El-Lahoun. Nous y trouvons deux algorithmes correspondant à des conceptions différentes des greniers à base circulaire de volume équivalent. Pour la première, on conserve la hauteur et on diminue le diamètre tandis que la seconde vise à diminuer la hauteur et à augmenter le diamètre. La première procédure est appliquée lors des mesures de superficie pour laquelle l’Auteur du Papyrus Rhind donne une monstration de sa validité. Nous étudierons les textes afférents. Papyrus Rhind (R41, R42, R43, R48 et R50) et Fragment UC32160-2 (= K LV4) d’El-Lahoun

Notre objectif est de proposer des activités pour nourrir un enseignement des aires fondé sur des expériences. Pour cela, notre approche repose sur l’introduction d’une perspective historique des contenus enseignés au lycée. Les membres du groupe ont élaboré plusieurs séquences pédagogiques expérimentées dans des classes de lycée. L’objectif des activités est de favoriser la compréhension de l'analyse en donnant une approche géométrique, instrumentale et technologique de l'intégration. L'obtention de cet objectif s'appuie sur les liens et les ponts mis en évidence entre domaines mathématiques et disciplines enseignées au lycée, en particulier les sciences de l'ingénieur et l’enseignement technologique. Nous proposerons aux participants de travailler sur des documents historiques et sur du matériel pédagogique proposé aux élèves. Le but est que les participants, réunis par groupes de niveaux scolaires, élaborent des activités pour la classe sur les thèmes suivants : 1) Recherches des aires rectilignes, sans formule et par équivalence géométrique d’aires. 2) Calculs des aires sous des arcs de parabole en confrontant différentes méthodes : méthode mécanique d’Archimède, méthodes des indivisibles. 3) Utilisation d'instruments pour déterminer des aires : les planimètres (que nous apporterons).

• Archimède, La méthode relative aux théorèmes mécaniques, Œuvres complètes d’Archimède (trad. Paul Ver Eecke), tome III. Éd. les belles lettres, Paris, 1971, p.477-484.
• Arnauld, Nouveaux Éléments de géométrie, Paris, 1667, p.305-309 et p.443-444
• Gilles-Personne de Roberval, Traité des indivisibles, Recueil de l’Académie des Sciences, Paris, 1693, p.257-259.

Avec les nouveaux programmes de collège de 2016, les triangles semblables ont fait leur réapparition au cycle 4, mais comment les intégrer à l’enseignement existant ? Quelles stratégies pour les enseigner en lien avec le théorème « de Thalès», les homothéties, les agrandissements-réductions? Ces notions semblent proches et difficiles à organiser au sein d’une progression au cycle 4. Les repères de progressivité contenus dans les programmes officiels recommandent l’enseignement du théorème « de Thalès » en classe de Troisième, mais ce théorème a-t-il encore une quelconque utilité ? Sa présence ne constitue-t-elle pas un obstacle supplémentaire pour le professeur lors de la conception d'une progression ? Comment et pourquoi introduire ce fameux théorème ? Nous tenterons de mettre en évidence les difficultés et les enjeux liés à l’enseignement de la proportionnalité en géométrie au cycle 4 grâce à des lectures de textes historiques mais également par l'analyse de productions d'élèves ou d'étudiants fonctionnaires stagiaires. Cet atelier s'adresse principalement aux enseignants de collège et de lycée mais pourra également intéresser les collègues du premier degré. Il est particulièrement adapté aux collègues qui ne sont familiers avec la lecture de textes historiques.

• Éléments d'Euclide (livre VI), la Géométrie de Descartes, les Éléments de géométrie de Clairaut.

À partir d’un matériel historique (puzzles et Tangram), cet atelier proposera des séquences actuelles et testées pour l’école primaire (maternelle et élémentaire). Dans un premier temps, les participants manipuleront le matériel proposé à des élèves de maternelle, de CE2 et de CM ; s’en suivra un temps d’échange. Dans un second temps, nous exposerons les spécificités de chaque classe lors des séquences de géométrie. Nous aborderons les compétences mathématiques, les procédures des élèves, la progression et la place du matériel. Nous terminerons sur la mise en place de séances de différenciation pédagogique afin d’atteindre les objectifs fixés en créant des interactions entre les différentes progressions. L’atelier est plus particulièrement conçu pour les enseignants du premier degré. Il exige une salle assez grande pour pouvoir constituer des groupes et manipuler.

• Maths et puzzles, brochure de l’APMEP n°1009, septembre 2016
• Mathematical games de Martin Gardner, scientific american 1974
• Regard Logique et calcul Tangram de Jean- Paul Delahaye, Pour la science n° 398
• La « procédure » du Gougu d’ Arnaud Gazagnes publié par l’IREM de Reims en 2005

Dès la seconde moitié du 16e siècle, la vogue italienne des jardins de plaisance se diffuse en France, comme en témoigne le succès du Songe de Poliphile (Venise, 1499 ; Paris, 1546), qui décrit la voyage d’un jeune homme à travers des jardins imaginaires jusqu’à l’île de Cythère à la recherche de la femme qu’il aime. Le jardinier devenant architecte doit pouvoir comprendre et effectuer lui-même des tracés communs de géométrie pratique en fonction des contraintes du terrain : perpendiculaire à une droite donnée passant par un point donné, bissectrice d’un angle, construction d’un triangle de côtés donnés, etc., jusqu’à la fameuse « ellipse du jardinier ». L’atelier est conçu en trois temps : 1° présentation des ouvrages français du 17e siècle sur le jardinage, 2° présentation d’activités réalisées du cycle 1 au cycle 4 et en formation initiale et continue d’enseignants, 3° manipulation des outils et réalisation de plans de jardins. Il est plus particulièrement conçu pour les enseignants du premier degré.

• Elie Vinet, L’Arpenterie. Bordeaux, Simon Millanges, 1577
• Samuel Marolois, Geometrie contenant la theorie et practique d’icelle necessaire a la fortification. La haye, Hendrik Hondius & Joann Jansson, 1616.
• Allain Manesson Mallet, La Geometrie pratique, tome troisième. Contenant la Planimétrie, ou la mesure des Superficies (ce qu’on appelle l’Arpentage), avec les Methodes de transfigurer, d’augmenter, & de diviser toutes sortes de Terres, Bois, &c. Paris, Anisson, 1702.
• Antoine Joseph Dézallier d’Argenville, La Theorie et la Pratique du Jardinage, où l'on traite à fond des beaux jardins appelés communément les Jardins de Propreté, comme sont les parterres, les bosquets, les boulingrins, &c. Paris, Jean Mariette, 1709.

L’atelier débutera par la présentation de la démarche, qui fait partie d’une recherche ayant pour finalité de retrouver les connaissances et les gestes professionnels des artisans de l’Antiquité, sujet sur lequel il n’existe aucun document écrit ou graphique contemporain. Il s’agit de tenter de restituer les modèles mis en œuvre par les mosaïstes antiques pour mettre en place les décors géométriques. Un document fiable permet de repérer des propriétés géométriques, conduisant à la proposition d’un modèle qu’on peut ensuite étudier dans le but d’en proposer un (des) algorithme(s) de construction et, au-delà, une procédure de mise en place in situ à l’aide des instruments de l’époque : cordeau, règle non graduée, équerre.
Les participants seront invités à travailler sur plusieurs exemples à l’aide des instruments de géométrie usuels et − s’ils l’ont à disposition − d’un logiciel de géométrie. Ils pourront ainsi prendre conscience des problèmes qui peuvent se poser à divers moments de la démarche.
Cette démarche peut être entreprise dans les classes, en fin de primaire ou au collège. Elle conduit à passer de l’objet matériel à un modèle, et éventuellement de celui-ci à une nouvelle réalisation matérielle (dessin en vraie grandeur au sol) qui pourra être comparée à l’originale, mettant en évidence les paradigmes géométriques qui se succèdent dans la scolarité obligatoire et leur articulation. À l’issue de la partie expérimentale, un débat sera engagé pour chercher à préciser comment cette démarche peut être utilisée en classe et/ou en formation d’enseignants.
Etant donné le sujet, il n’existe aucun document d’époque (à part un texte de Vitruve sur la composition de l’assise du pavement), et c’est précisément là le challenge qui se pose à nous. Les documents sur lesquels s’appuiera l’exposé et travailleront les participants seront des clichés photographiques de mosaïques.

• Malek, A.-A., Parzysz, B. (2016) Les mosaïques « kaléidoscopiques » de Numidie. Bulletin de l’APMEP 521, 554-561.
• Parzysz, B. (2009) Key digrams to design and construct Roman geometric mosaics? Nexus Network Journal 11/2, 273-288. Ed. Birkhaüser, Basel.
• Parzysz, B. (2012) Une grande famille de décors géométriques. Proceedings of the 11th
International colloquium on ancient mosaics (M. Šahin, ed.). Ed. Zerobooks (Istanbul), 735-748.
• Parzysz, B. (2012) La géométrie de la mosaïque de Penthée (Nîmes). Bulletin de l’APMEP 500, 420-428.
• Parzysz, B. (2014) Une composition géométrique étonnante : la mosaïque de Lod (Israël). Bulletin de l’APMEP 509, 295-308.
• Parzysz, B. (2016) De la nécessité d’identifier précisément le décor géométrique d’une mosaïque. Une étude de cas. Journal of Mosaic Research 9, 47-58.
• Parzysz, B. (2017) La géométrie des mosaïques de Neptune et de Méduse : thèmes, variations, adaptations. Le quartier antique du Palatium et ses domus. Archéologie au collège Lumière à Besançon (Doubs) (C. Munier, dir.). Presses Universitaires de Franche-Comté, Besançon, 289-297.
• Vitruve, De l’architecture. Livre 7. I. De la rudération. Trad. Ch.-L. Maufras, tome second, 119-123. Ed. Pancoucke, Paris 1847

Encouragée à la fin du XVIIIe siècle par Mirabeau et Condorcet, puis introduite dans les programmes d’enseignement secondaire à partir de 1809, puis primaire en 1833, la géométrie pratique est ensuite enseignée durant la Troisième République. Recommandée en été, décrite comme une activité attrayante pour les élèves et un complément idéal de leçons purement théoriques et abstraites, elle emploie des instruments comme le graphomètre et l’équerre d’arpenteur. L’atelier donnera l’occasion aux participants de manipuler ces instruments pour effectuer mesures de distances inaccessibles, arpentage et levés de plan. Une analyse des raisons de l’utilisation de problèmes pratiques dans l’enseignement de la géométrie au XIXe siècle et des comptes rendus d’expériences récentes en classe à l’école et au collège complèteront les expérimentations sur le terrain. L’atelier est plus particulièrement conçu pour les enseignants du premier degré. Prévoir 7 à 8 décamètres et 4 jalons.

• Buisson Ferdinand (dir.) (1887) Dictionnaire de pédagogie et d’instruction primaire, tome 1, Paris, Hachette.
• Eysséric Joseph (1855) Notions de géométrie pratique et d’arpentage à l’usage des élèves qui passent de l’école primaire aux champs ou à l’atelier, Paris, Langlois et Leclercq.
• Cazeneuve Frère Irlide (F. I. C.) (1882) Manuel d’arpentage pour les écoles primaires, Tours, Mame et fils.
• Guilmin Adrien (1861) cours élémentaire de trigonométrie rectiligne : à l’usage des lycées et des collèges, Paris, Durand.
• Laisant Charles-Ange (1915) L’initiation mathématique, 14e édition, Paris, Hachette.
• Pécherat Joseph (1897) La géométrie pratique, arpentage et cubage à l’usage des Écoles primaires, des Cours d’adultes et des Familles, Châteauroux, Badel.
• Puille David (1887) Cours complet d’arpentage élémentaire, théorique et pratique à l’usage des divers établissements d’instruction, 18e édition, Paris, Fouraut et Fils.
• Régnault Jean (1861), Manuel pratique d’arpentage à l’usage des instituteurs primaires, Paris, Mallet-Bachelier.

Après la naissance du calcul infinitésimal, les mathématiciens et les ingénieurs ont cherché à concevoir des instruments mécaniques pour effectuer concrètement les opérations du nouveau calcul et construire d’un mouvement continu les courbes transcendantes désormais admises en géométrie. En 1693, Leibniz lui-même a donné le schéma d’une sorte d’intégraphe universel permettant de réaliser les quadratures et de résoudre le problème inverse des tangentes. En fait, c’est surtout au XIXe siècle que sont inventés, fabriqués et diffusés des instruments mécaniques de précision au service de la géométrie transcendante. L’atelier proposera diverses activités pour faire découvrir l’histoire de ces appareils : lecture de textes originaux, exploration d’instruments particuliers (planimètre à cône, planimètre polaire, intégraphe, tractoriographe) à travers des vidéos, des simulations numériques et la manipulation d’exemplaires réels, constructions géométriques, justifications théoriques. Une réflexion sera proposée aux participants sur l’intérêt de s’appuyer sur certains de ces instruments pour faciliter l’acquisition des concepts fondamentaux du calcul intégral, notamment les notions d’aire et de primitive, en classe terminale et dans les enseignements post-bac. L’atelier demande quelques notions mathématiques sur le calcul intégral (niveau terminale)

• Gottfried Wilhelm Leibniz, Supplementum geometriæ dimensoriæ seu generalissima omnium tetragonismorum effectio per motum : similiterque multiplex constructio lineæ ex data tangentium conditione, Acta eruditorum, sept. 1693.
• Felix Klein, Leçons sur certaines questions de géométrie élémentaire, Paris, Novy, 1896.
• Louis-Frédéric Jacob, Le calcul mécanique, Paris, Doin, 1911.
• Henri de Morin, Les instruments d’intégration, Paris, Gauthier-Villars, 1913.